Theory of Measurements 4

     We are discussing the State of Measurement, in the discrete measurement space or j-space. Theories of Special Relativity and General Relativity, are our preferred tools of description.

    We have an observer/object making measurement at rest in S-frame and another observer/object being measured in S'-frame. The observer in S-frame, Obs_M, has the efficiency

η

.

We also have a hypothetical observer Obs_c, kind of relativistic Maxwell's Demon, whose geodesic lies on the light cone and this observer represents the maximum efficiency (η_c) observer in S-frame. The measurements of Obs_c, establish the basis vectors or the gradients, for the coordinate frames used by Obs_M.

The S-frame represents vacuum, while S'-frame represents vacuum +

δ

ecosystem, and therefore Obs_M is making measurements in curved space-time.

We take the normal

\widehat{n}

from S-frame and complete a measurement circuit M_ckt, in S'-frame. Turns out that

{\widehat{n}}_{i}

(initial) and

{\widehat{n}}_{f}

(final) are not congruent as shown below, due to the holonomy present in S'-frame geometry.

However, since M_ckt is completed, some sort of motion is possible. So now, we need to figure out what does this motion mean for a State of Measurement?

Let us consider a simple case of a State of Measurement, in which an electron is orbiting around a proton. We assume that the orbit of the electron is circular. We assign S-frame to the electron and S'-frame to the proton.

Fairly straightforward, as the electron assigned S-frame with observer efficiency

{η}_{e}

, is making measurement. The proton, having a more complex internal structure, i.e. a complex

δ

-ecosystem and therefore, is assigned S'-frame. The proton is being measured by the electron as shown below:

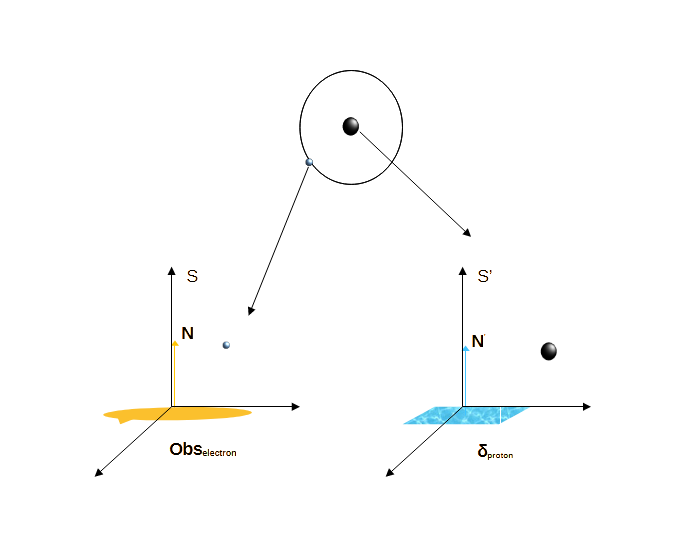
We also note that the electron has no idea about proton or S'-frame. It is merely making measurements in the measurement space setup by the observer with maximum efficiency Obs_c, in a field present due to the proton. (Actually the photon itself, which approximates Obs_c and who is setting up

{F}^{μν}{F}_{μν}

a.k.a. j-pixels in topological space, knows very little about the proton.)

In essence, Obs_c sets up the null {}, for the macroscopic observer(s) making measurements in S-frame, in this case an electron. Then a

δ

-function, information being measured, a proton, is introduced in this null space, represented by S'.

The force field which determines the motion of the observer (electron) and hence the geometry of motion, is setup by the δ-function or the proton.

The velocity of the electron is given by the Bohr's model as

{v}_{e} ∝ \frac{{e}^{2}}{ℏc}

, which is less than the velocity of light c.

↓

Any State of Measurement in discrete measurement space is considered equivalent to a stable system, while the measurement is in progress. Therefore we can use the Virial Theorem to estimate the potential energy of the electron as

{U}_{el}={m}_{e}{v}^{2}

↓

Using Sommerfield's interpretation of the fine-structure constant(α),

v=αc

, the potential energy of the electron while it is in the state of measurement, is given by

{U}_{e}={α}^{2}({m}_{e}{c}^{2})

v=αc

↓

In j-space, we can therefore write Lorentz's factor

γefor

                                                    the electron in
                                                    S-frame,

in terms of fine-structure constant

α

as,

γ=\left(1-{η}_{e}/{η}_{c}\right){}^{-1}=\left({1-{v}^{2}/{c}^{2}}\right)^{-1}={\left(1-{α}^{2}\right)}^{-1}

Thus, the fine-structure constant provides us with the information about the capability of the observer to make a measurement i.e. to complete the M_ckt in S'-frame and the expression for

γ

reflects that.

We will note that the efficiency of the observer representing a proton is unknown. (Interesting, how two dimensionless quantities related to apparently different relativistic physical phenomena, are connected to each other for an electron, which also does not have any known internal structure?)

The fine-structure constant

α

, plays an important role in discrete measurement space, as it allows us to determine resources required for an electron to make a measurement in information space of S'-frame.

When an electron completes a single M_ckt in S'-frame, a minimum momentum is transferred between the field and the electron (

α=1/137

. We note that, the minimum-momentum transfer is not the same as the zero-momentum transfer during a measurement.¹

Now let us, as an hypothetical case, increase the information content of the

δ

-function (>>proton) being measured in S'. Then the momentum being transferred between j-pixel and the observer, is much higher while completing the M_ckt. For example, the value of

α

= 1/128, represents the energy scale around 81 GeV (W-Boson).² The j-pixels are much finer, 2 x 10^-17 meters, compared to

\infty

(assumed for

α

= 1/137).

Thus the value of the fine-structure constant

α

, provides an observer in S-frame, with some sense of how difficult the problem of measurement can be for a given

δ

function in S'-frame. And, it also correlates the fundamental constants e, h, and c as

α∝\frac{{e}^{2}}{ℏc}

. But why does it have to be dimensionless?

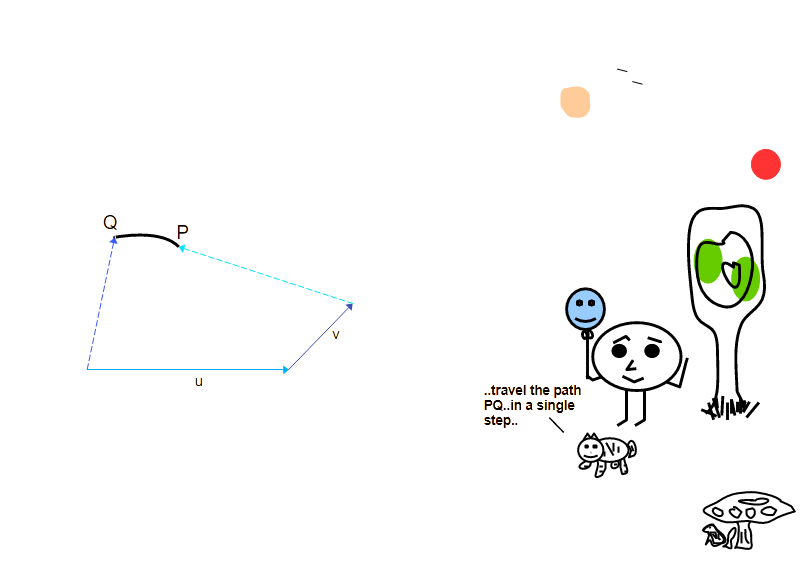
Let us assume that an observer (electron) is trying to determine the problem landscape. The observer has access to force (rate of change of momentum), clock, and rod. If the observer has force, then we can assign the momentum a direction

\widehat{n}

.

The electron completes a measurement circuit in S'-frame and finds out the direction of force has changed by

\frac{π}{2}

, as the circuit is completed. We can think of

{\widehat{n}}_{i}

and

{\widehat{n}}_{f}

, as the directions of force/momentum applied to make a measurement and the direction of the response (which is based on internal space of the

δ

-function in S'), respectively. [j-pixels created by Obs_c are trying to map this internal space in S'-frame.]

We can write the information extracted by the electron measurement (I_ckt) as,

{I}_{ckt}={k}_{S}[ln({1}_{j})-ln({Ω}_{ckt})];\; where\; ln({1}_{j})={0}_{j}.

Here

{Ω}_{ckt}

represents the entropy states of the electron, while measuring a

δ

-function in S'-frame. Let us say that the electron started measuring at instant

{0}_{j}

and the circuit was completed at

{0}_{j}+ϵ

. In our case, since the information contained within a proton, is assumed continuous for the electron, we use negative exponential distribution to write, (we have removed the subscript j from 0 and 1 from now onwards),

I_{ϵ} \propto I_{0} e^{- q}; (q t a k e s d i s c r e t e v a l u e s),

{I}_{ϵ}∝{I}_{0}{e}^{-q};\;(q\,takes\, discrete\, values).

{I}_{ckt}={I}_{ϵ}.

Thus we have two important parameters based on the problem landscape,

{Ω}_{ckt}

and q. Here the entropy

{Ω}_{ckt

results in

\frac{π}{2}

shift for

\widehat{n}

, once a single measurement circuit is completed in S'⁴.

And q represents the information being measured as one measurement circuit is completed. So how do we correlate

{Ω}_{ckt}

and q?

Let us define a parameter X = exp^(1-q), where q takes positive integer values, and increasing q-value means an observer of diminishing capabilities. We have made an assumption that the S'-frame information space is continuous for the electron measuring it.

↓

Next, define Y as the ratio of X and

\frac{π}{2}

(in radians) for increasing q values. At this point, we already know that something funky is going on as the response to electron measurement force direction (

\widehat{n}

), is shifted by

\frac{π}{2}

in S-frame, where electron is at rest.

We need to determine the q value to know why the shift? If the q value was 1 for the electron, then X would have been 1, i.e. all the information from S', could be measured by the electron in S-frame. But, clearly that is not the case.

↓

Next we square Y values for different q values.⁵ We get the following:

q	Y²
1	1/2.468
2	1/18.236
3	1/134.750
4	1/995.679

We keep in mind that what we have so far, is just a rough approximation and we have not really correlated Y² to any other known measurements made by the electron in S-frame.

↓

We have another piece of information, which is the energy level splitting in H-atom. And explaining this energy level splitting, requires a constant

α∼\frac{1}{137}

. Nice! Y² is

∼\frac{1}{135}

. So what does it tell us?

Very clearly with low

α

-values, the electron can not extract all the information contained within the proton structure, which apparently has a very complex ecosystem of

δ

-functions. And therefore, the electron is likely to stay in the orbit. Thus the electron-proton structure stays stable, while the electron is in the state of measurement.

Furthermore, it also gives us a sense that electron-photon interaction alone is not sufficient to probe, proton structure with complete precision. The j-pixels setup by photons is too coarse. (Also, photons may move at the speed of light, but how many of them will be created by an electron, depends upon the fine-structure constant.)

Based on what we know so far, getting to the technologies required to measure the information structures corresponding to q = 2 or q = 1, is virtually impossible as

α

values are very high. We could just look at the gigantic ATLAS, which determined the existence of W-boson at

{α}_{{m}_{w}}=\frac{1}{128}

.

So is the challenge we have, to build a functioning device corresponding to

α=\frac{1}{134}

. Although there are some theoretical constructs, such as Quantum Spin Ice predicting extremely high

α=\frac{1}{10}

.

We have been discussing the rate of change of momentum of an observer in S-frame, and how it shifts by

\frac{π}{2}

as a measurement is made? Momentum represents the charge q_e, and we do assume E and B at an angle

\frac{π}{2}

to each other.

    Thus the fine-structure constant can be connected to the curvature(holonomy) of the information landscape in S'-frame, being measured in the discrete measurement space of S-frame.

    It reflects how much the direction of the measurement force shifts due to the curvature (~ $π$ /2 for example), when a measurement circuit is completed by the observer (an electron in S-frame).⁶

   We have indirectly discussed the phenomenon of the electromagnetism. The Ampere-Maxwell law is given as,

∇×\widebarB = {μ}_{0}(\widebarJ+\frac{∂\widebarD}{∂t}).

    In above equation J represents the current density and in j-space, it represents the physical motion of the observer (an electron) in S-frame.

    The quantity D, the displacement vector, represents M_ckt for the electron in S'-frame.

    We need to remember that in the state of measurement, two types of dynamics are involved, the actual physical motion in S-frame, the current density J in Ampere's law, and the measurement progression in S'-frame, the time derivative of D or Maxwell's displacement current.

    Unless the measurement progresses in S'-frame information space, the physical motion of the observer in S-frame is not possible.

....to be continued

______________

1. Actually, a Zero-force/momentum measurement does not exist in j-space, as even a single measurement requires a finite force/momentum (= 0_j). We call such measurement a Zero-Entropy measurement. Zero-momentum measurement is equivalent to Parallel Transport, and it is not possible in the presence of a δ-function in S'-measurement space.

2. If we look at the energy and space scales between

α

= 1/137 and

α

= 1/128, there is an enormous gap, and we have barely modified the observer's capability (

∼{α}^{2}

). A warp drive require

η

= 1. With the resources presently available to us, we can not even reach required energy scales, let alone maintaining a stable state of measurement. How about Warp-9 then?

3. We will discuss this part later.

4. A completed measurement circuit, is not equal to an orbit.

5. Why square Y? The electron has seen the shift in momentum direction,

\frac{π}{2}

, as M_ckt is completed, however the electron is still in a state of measurement. And we can determine the resources in a state of measurement, only as energy. So the dimension analysis requires that we look at Y (equivalently Force or Momentum) and Y² (equivalently Energy) both. Y and Y², both are dimensionless. (The physical constants e, h, and c are not used to derive Y².)

6. In GR the holonomy represents, the curvature in time-space which in turn results in the gravitational force.

The Theory of Measurements - IV

Previous Blogs: