An ethereal energy source in Blip
19th July 2020
"Why, for example, do we still not have an international center for climate predictions, which by current estimates would cost “only” $1 billion spread over 10 years? That’s peanuts compared to what particle physics sucks up, yet vastly more important. Or why, you may have wondered recently, do we not have a center for epidemic modeling?
It’s because too much science funding is handed out on the basis of inertia. In the past century, particle physics has grown into a large, very influential and well-connected community. They will keep on building bigger particle colliders as long as they can, simply because that’s what particle physicists do, whether that makes sense or not.
It’s about time society takes a more enlightened approach to funding large science projects than continuing to give money to those they have previously given money to. We have bigger problems than measuring the next digit on the mass of the Higgs boson."
- Sabine Hossenfelder in The World Doesn’t Need a New Gigantic Particle Collider, Scientific American, June 19, 2020.
***
So far we have
developed the idea of a discrete
measurement space or j-space, which is
solely based on the physical
measurements of an infinite source.
Since physical measurements do not
allow the precise determination of
origin, j-space has to have lower
bounds for the measurements of various
physical quantities. Similarly
upper bounds must also exist.
In j-space the resource management is very important and different observers have different resources and thus different capacities to perform precise measurements. The observer Obsc, with measurement capacity (v2/c2 ~1), determines the lower and the upper bounds, based on which the guidelines for the measurements in Aku's universe Blip, are established.
The fabric of j-space consists of j-pixels, which we have discussed earlier. In next few blogs we will be discussing, how to introduce physical structures, cosmic and elementary both, in j-space fabric. We will be using basic quantum mechanics concepts, such as Levinson's theorem, bound states and δ-potentials, along with Kruskal-Szekeres coordinates, in j-space.
δ-potentials and bound states:
The presence of δ-potentials and subsequent bound states for a particle, is a standard problem in Quantum Mechanics. The case of a single delta potential and the corresponding bound state for a particle of mass m, is shown below:
In j-space the resource management is very important and different observers have different resources and thus different capacities to perform precise measurements. The observer Obsc, with measurement capacity (v2/c2 ~1), determines the lower and the upper bounds, based on which the guidelines for the measurements in Aku's universe Blip, are established.
The fabric of j-space consists of j-pixels, which we have discussed earlier. In next few blogs we will be discussing, how to introduce physical structures, cosmic and elementary both, in j-space fabric. We will be using basic quantum mechanics concepts, such as Levinson's theorem, bound states and δ-potentials, along with Kruskal-Szekeres coordinates, in j-space.
δ-potentials and bound states:
The presence of δ-potentials and subsequent bound states for a particle, is a standard problem in Quantum Mechanics. The case of a single delta potential and the corresponding bound state for a particle of mass m, is shown below:

The bound state Eb
is same as the ground state if the
potential is symmetric. If there
are more than one delta functions,
there can be more than one bound
states depending upon the magnitude of
αδ(x). Our
objective in next few blogs, is to
discuss the basic assumption
behind the discrete measurement space
or j-space, that every object in
j-space is in a state of measurement,
thus performing a measurement as well
as being measured itself.
Why do
elementary particles exist in
j-space, to begin with?
Let us review the expression for the bound state energy in the presence of a delta function:
Let us review the expression for the bound state energy in the presence of a delta function:

The important
quantities here are m, α, and ħ. But
first we need to understand what do
we mean when we make the statement
that "a particle of mass m exists"?
In a measurement space, a measurement is completed when the corresponding circuit is
completed i.e. the observer
has arrived back at its point of
origin.
is
completed i.e. the observer
has arrived back at its point of
origin.
In the discrete measurement space the objective is to measure the Least-Energy Surface (LES) with the absolute precision, but clearly not all the observers can perform this measurement. We also note that the physical world exists in region-I of Kruskal-Szekeres coordinates, shown below:
In a measurement space, a measurement is completed when the corresponding circuit
 is
completed i.e. the observer
has arrived back at its point of
origin.
is
completed i.e. the observer
has arrived back at its point of
origin. In the discrete measurement space the objective is to measure the Least-Energy Surface (LES) with the absolute precision, but clearly not all the observers can perform this measurement. We also note that the physical world exists in region-I of Kruskal-Szekeres coordinates, shown below:

The position of
the measurement circuit in
Kruskal-Szekeres coordinates is around
the Event-Horizon Point (EHP), Rsch
= 2MG. In the following diagram
various measurement circuits around
EHP are shown. We note that the
conventional space and time exist in
the external Region-1 only, or in
other words a macroscopic observer ObsM, exists in the
external Region-I only.

The measurement
circuits are shown in blue. The
macroscopic observer's capability to
make measurements is decreasing as we
move from the left to right in the external
Region-1, and it is
represented by the hyperbolic paths in
black. Sharper the curvature at
the vertex, more difficult the
measurement, i.e. more and more
resources are needed to make a
measurement as we move from the right
to the left in the external Region-1.
In j-space, the
measurement circuit is around LES and
the intersection of an hyperbola and
an arc of measurement circuit (shown
in red) in the external Region-1, represents the
measurement of an elementary particle,
made by ObsM1.
Thus
we have elementary particles
corresponding to each red-arc (or
equivalently the part of a
blue-measurement circuit in Region-I)
which potentially can be measured by a
macroscopic observer ObsM,
given ObsM has sufficient
resources to measure it2.
In the following diagram, an observer
can measure m2
and m3, but
not m1.
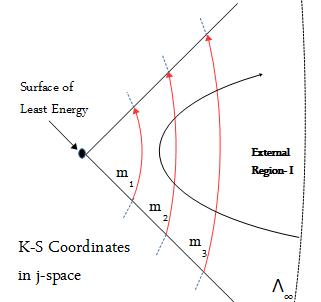
To measure the particle m1, the observer making measurement needs to be provided additional resources in the external Region-1. This situation is shown by the dashed path in the following diagram.

This is what particle-colliders
are trying to do in a rather
rudimentary way. However it must be
clearly understood that no matter how
much resources are provided to an
observer making measurements in the
external region-1, LES can never be
measured with an absolute
precision.
At best we will have an enormous catalog of particles, afflicted with la maladie exotique, but no new fundamental principle is likely to be discovered. For that we will have to analyze, and predict, the results obtained by Astronomy and Cosmology.
Nature of bound states in j-space
At best we will have an enormous catalog of particles, afflicted with la maladie exotique, but no new fundamental principle is likely to be discovered. For that we will have to analyze, and predict, the results obtained by Astronomy and Cosmology.
Nature of bound states in j-space
Let us consider an observer ObsM in
j-space, with
resources in the range (Ei,
Ef). Providing
a precise value of the energy to an
observer in j-space is not possible,
as it implies ΔE =
0. According to uncertainty
principle, ΔEΔt
> ħ, ΔE
= 0 means a state
with infinite life-time is measured by
ObsM. An
infinite life-time measured by ObsM, is finite (∞j) per the
measurements of Obsc or Obsi, and hence Δt
is always finite and subsequently ΔE
is always greater than 0.
The observer ObsM will be measuring the potentials ranging from a shallow-well to a deep-well as shown below:
The observer ObsM will be measuring the potentials ranging from a shallow-well to a deep-well as shown below:

We note that as
the depth of the potential well
increases the observer ObsM
has less and less freedom in the free
space.
Next we consider an observer Obsc who has infinite, ∞j, resources in j-space. This observer Obsc will have values for energy ranging from 0j to ∞j, in j-space corresponding to the current information space (q = 3). We want Obsc to measure a shallow- potential well in a higher information space (q = 2).3 In other words we want Obsc, if possible, to perform a zero entropy measurement in q = 2 information space.
Next we consider an observer Obsc who has infinite, ∞j, resources in j-space. This observer Obsc will have values for energy ranging from 0j to ∞j, in j-space corresponding to the current information space (q = 3). We want Obsc to measure a shallow- potential well in a higher information space (q = 2).3 In other words we want Obsc, if possible, to perform a zero entropy measurement in q = 2 information space.
For Obsc since it has ∞j resources, all the potential wells in q = 3 information space, are equivalent to shallow-wells and represent zero-entropy measurements. However in the case of q = 2 information space, the situation becomes rather interesting. A shallow-well in q = 2 space is equivalent to δ-potential in q = 3 space even for Obsc. And δ-potential is, what Obsc is measuring even though Obsc has infinite, ∞j, resources in q = 3 space, as shown below:

In this case, all the states are inside the δ-potential and they form in essence a single bound state or a "coherent" state of the width ΔE ~ 0. Thus the nature of the bound state in q = 3 measurement space, while measuring a shallow well from q = 2 space, is that of a coherent state Ecoh.
The measurement of δ-potential in Blip
Our interest is in understanding how the measurements of the coherent state Ecoh, manifest themselves into physical parameters measured in Blip. Blip is represented by the measurements made by the macroscopic observer ObsM, in the external region-I in K-S coordinates.
Since the energy of the coherent state Ecoh in q = 3 information space, has a minimum limit ∞j, the corresponding rest mass mo = E × (c2)-1, will be infinite or extremely heavy, even though the physical dimensions may be in Planck's domain, in the q = 3 space or equivalently in the external region-I of KS Coordinates.
The coherent state will have a minimum spread ΔEcoh ~ 0j, per ObsM measurements. The uncertainty principle correlates ΔEcoh with the coherent state life-time tcoh in external region-I, as ΔEcoh × tcoh ~ ħ. Since ΔEcoh is very small, the coherent state life-time tcoh will be exceeding large (~∞j).
Next, in external Region-I, an infinitesimal change in entropy of the coherent state dScoh and the change in the energy to bring about the infinitesimal change dScoh in the entropy dEcoh, are correlated to the temperature Tcoh of the coherent state as:

It will take
infinite amount of resources (dEcoh
~ ∞), to bring about
infinitesimal change in the entropy
(dScoh
~ 0), of the coherent state under
discussion. Hence the
temperature of the coherent state as
measured by the macroscopic observer
ObsM,
will be exceedingly high.
Finally an infinite energy-source in Blip
Therefore in the discrete measurement space, the shallow-well from a higher-information-space|q=2 is equivalent to a δ-potential in the current-information-space|q=3. The information corresponding to the shallow-well|q=2, will be measured as a coherent-state|q=3 by a macroscopic observer ObsM, in Blip (equivalently q=3 information state or the external region-I of KS coordinates).

This coherent state
will result in an extremely massive
entity in Blip, with an infinite
life-time and infinite
temperature. The infinite-ness
of the coherent state Ecoh, disappears as Ecoh slowly radiates
away, in the external Region-I (in a
few billion years probably).
Lastly, the "measured-mass" and the temperature of the coherent state, as they are determined in Blip, are statistical quantities inversely related to the spread in the energy ΔEcoh, of the coherent state|q=3, similar to the life-time tcoh.
Finally an infinite energy-source in Blip
Therefore in the discrete measurement space, the shallow-well from a higher-information-space|q=2 is equivalent to a δ-potential in the current-information-space|q=3. The information corresponding to the shallow-well|q=2, will be measured as a coherent-state|q=3 by a macroscopic observer ObsM, in Blip (equivalently q=3 information state or the external region-I of KS coordinates).

Lastly, the "measured-mass" and the temperature of the coherent state, as they are determined in Blip, are statistical quantities inversely related to the spread in the energy ΔEcoh, of the coherent state|q=3, similar to the life-time tcoh.
____________________
1. The physical world of Blip, exists at Λ-plane.
2. Action in j-space is defined as the resources provided to an observer traveling the path PQ, at the point P, such that the observer can arrive at the point Q unassisted. In external region-I of KS coordinates, action translates into the physical variables, energy E or the momentum k.
3. Different information spaces do not agree upon the definitions of Lorentz and Möbius invariances.
1. The physical world of Blip, exists at Λ-plane.
2. Action in j-space is defined as the resources provided to an observer traveling the path PQ, at the point P, such that the observer can arrive at the point Q unassisted. In external region-I of KS coordinates, action translates into the physical variables, energy E or the momentum k.
3. Different information spaces do not agree upon the definitions of Lorentz and Möbius invariances.
***
To be continued..
Previous Blogs:
Nutshell-2019
Stitching the Measurement Space - III
Stitching the Measurement Space - II
Stitching the Measurement Space - I
Mass Length & Topology
Chiral Symmetry
Sigma-z and I
Spin Matrices
Rationale behind Irrational Numbers
The Ubiquitous z-Axis
Majorana
ZFC Axioms
Set Theory
Nutshell-2014
Knots in j-Space
Supercolliders
Force
Riemann Hypothesis
Andromeda Nebula
Infinite Fulcrum
Cauchy and Gaussian Distributions
b-Field & Lower Mass Bound
Incompleteness II
The Supersymmetry
The Cat in Box
The Initial State and Symmetries
Incompleteness I
Discrete Measurement Space
The Frog in Well
Visual Complex Analysis
The Einstein Theory of Relativity
***
Sigma-z and I
Spin Matrices
Rationale behind Irrational Numbers
The Ubiquitous z-Axis
Majorana
ZFC Axioms
Set Theory
Nutshell-2014
Knots in j-Space
Supercolliders
Force
Riemann Hypothesis
Andromeda Nebula
Infinite Fulcrum
Cauchy and Gaussian Distributions
b-Field & Lower Mass Bound
Incompleteness II
The Supersymmetry
The Cat in Box
The Initial State and Symmetries
Incompleteness I
Discrete Measurement Space
The Frog in Well
Visual Complex Analysis
The Einstein Theory of Relativity
***

Attribution — You must give appropriate credit, provide a link to the license, and indicate if changes were made. You may do so in any reasonable manner, but not in any way that suggests the licensor endorses you or your use. No additional restrictions — You may not apply legal terms or technological measures that legally restrict others from doing anything the license permits. This is a human-readable summary of (and not a substitute for) the license.


