The Theory of Measurements - V
Physics in Action
15th April 2025
"The principle of Least Action is this: Of all the different sets of paths along which a conservative system may be guided to move from one configuration to another, with the sum of its potential and kinetic energies equal to a given constant, that one for which the action is the least is such that the system will require only to be started with the proper velocities, to move along it unguided."
- Lord Kelvin and P. G. Tait, Treatise on Natural Philosophy, 1912.
“Also, I should say that S is not really called the ‘action’ by the most precise and pedantic people. It is called ‘Hamilton’s first principal function.’ Now I hate to give a lecture on ‘the-principle-of-least-Hamilton’s-first-principal-function.’ So I call it ‘the action."
- R. P. Feynman, The Feynman Lectures on Physics.
"Therefore a priori a point motion is conceivable, for which the four-dimensional path of the point would be an almost closed one. In this case one and the same material point could be present in an arbitrarily small space-time region in several seemingly mutually independent exemplars. This runs counter to my physical imagination most vividly. However, I am not able to demonstrate that the theory developed here excludes the occurrence of such paths.”
- Einstein, as quoted by John Stachel in AMS Review of A World Without Time: The Forgotten Legacy of Gödel and Einstein.
When we assigned the frames S and S' to the observer and the system being measured respectively, we made a rather abstract assumption of their relative capabilities. It was not clear where did the conventional physics come in to the picture?
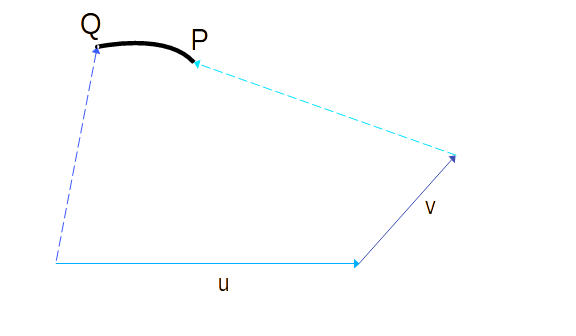
Let us assume an observer making a measurement, is moving on a path PQ. The path PQ could be either a straight line or a curve.

The simplest case, is that of an observer being a free particle with the Kinetic Energy T. And if the observer has taken time to travel the path, then required resources are equal to T (joules-second).
In physics, the quantity representing the minimum Kinetic Energy T required to travel the path PQ or equivalently to complete a measurement, is called Action S. In the case of a free particle we just described, the action S is equal to T.
Here nature being frugal1, requires the observer to choose the path which requires the least amount of resources to travel from P to Q. For a free particle, that path is straight line and we have assumed that the Kinetic Energy T, remained constant throughout the measurement. Therefore action S is a simple product of T and Δt.
However for the measurements made on a -ecosystem in the S'-frame, the observer in S-frame, can not be assumed equivalent to a free particle. There is this enormous amount of Potential Energy V, influencing the measurements or figuratively the motion along the path PQ, which needs to be accounted for, before an observer can start moving from P to Q or equivalently start extracting information about a structure in S'-frame. The observer's Hamiltonian H = T+V, accounts for the resources needed for the specific observer.
The conventional physics or the information about the universe as we understand it, is incorporated within the action S, combined with the Principle of Least Action (). We can correlate the Hamiltonian H and the Action S for the path PQ for a given observer, using Hamilton-Jacobi Equation, which eventually leads to Schrödinger's wave equation.
By traveling the path PQ, we are looking to extract information about the structures represented by the curved path PQ. However our ultimate goal, is to find the path represented by a straight line connecting P and Q, which is enormously difficult at small scales nearing Planck dimensions.2
Clearly, an extraordinary amount of resources are required to fully analyze a complex singular or composite -ecosystem. Unless we improve the value of , with a completely different mechanism or equivalently reduce the value of V in action S (S = T - V), with current existing capabilities we will be forced to build more and more complex machinery, to probe sub-atomic structures with precision.
This approach of increasing technical complexity, actually does not follow the principle of least action for a free particle, as in this case P and Q are not connected by a straight line!
The concept of time, is quantitative in the discrete measurement space or j-space. Let us 'Gedankenexperiment' in terms of observers making measurements in S-frame. We have 'Aku' and 'The Bug on the windshield' (TB), as observers3. And we ask them to identify the geometric structure shown below:
The geometric structure is assigned S'-frame, while Aku is in ts own rest frame SAku, and TB is in its own rest frame STB.
For Aku, it is straightforward, a circle. One measurement and the state of measurement is over, i.e. zero-entropy measurement. The time taken to perform this single measurement, is infinitesimal but finite. And Aku is free to perform next measurement on slinky.
However for TB, situation is impossible with no prior knowledge of geometry and a very limited Hamiltonian (T+V). Furthermore, there is no guarantee that TB would arrive at the same conclusion as Aku, once its measurements are completed.
In fact, if we looked at the same measurement millions of years from now, TB and its descendants (TBs), will still be in a state of measurement, with generations would have passed with no change, as if the time stood still for them. And this would not be a time-dilation effect either.
So, for TBs the state of measurement becomes an epoch, while for Aku it is a zero-entropy measurement. (The circle or equivalently the -function being being measured in S'-frame in this case, remains unchanged.)
For us the humans, the situation is not very different. The universe is in a state of measurement. What we humans consider an epoch (S-frame), is a mere blip in actual epoch (S'-frame), of whose true nature we have no idea about, as our Hamiltonian itself is fairly limited.
The time as an universal parameter has meaning only in Galilean universe, where frame of references are inertial for all observers (examples: the colony of TBs, a rock).
The problem we are discussing, that of an electron in a state of measurement of a proton, the time & the space definitions are entirely different for either of them, as each is an observer with its own capability defined by varying values of .
In a discrete measurement space therefore, we can state the following about time:
1. Time must exist in a measurement space, because even the zero-entropy measurement which is a single measurement, requires time, however infinitesimal it may be. (The zero entropy measurement, is not possible without prior knowledge, which has its own time-axis.)
2. Time span/epoch depends upon the observer's capability or resources (H), and the complexity of the object under measurement or its information content (S = T-V).
3. A universal definition for time, is relevant only in the Galilean universe where the frame of references are inertial for all observers.
Let us go back to the problem of measurement we had been discussing. we note that the electron has no physical sense of the presence of proton, except for the fact that it is moving in a field setup by the proton.
There are observers of varying capabilities who also measure the proton. The vector space V, we are so familiar with, is set up by the observer with maximum capability Obsc, = 1.

The measurements of the electron in its own time and space are performed in the covector space V*, corresponding to the observer with .4
The electron in S-frame will not know the difference if we replaced the proton with a battery in S'-frame, except that its trajectory will change.
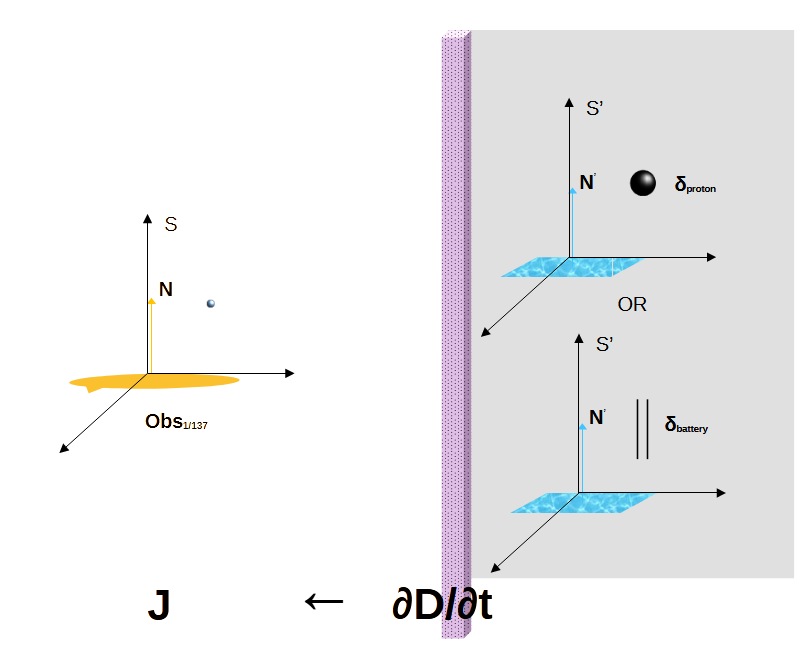
 Note that we will be
replacing the indices with
the observer capabilities in
terms of α. So Obsc
()
becomes Obs1.
Similarly Obse ()
becomes Obs1/137.
The Maxwell's Demon remains
Obsi.
Note that we will be
replacing the indices with
the observer capabilities in
terms of α. So Obsc
()
becomes Obs1.
Similarly Obse ()
becomes Obs1/137.
The Maxwell's Demon remains
Obsi. The
electron in S-frame
moving under the
influence of proton or
nucleus in S'-frame,
will follow a circular
orbit. By
spherical symmetry, the
electron has equal
probability of being on
any of the great circles
on a sphere. (Check
out the linked video
on Hopf Fibration.)
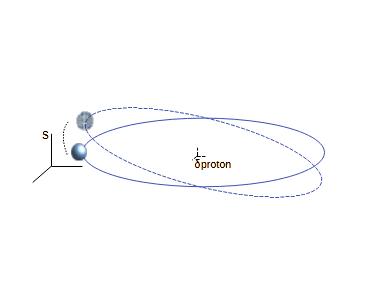
The
electron in S-frame
moving under the
influence of proton or
nucleus in S'-frame,
will follow a circular
orbit. By
spherical symmetry, the
electron has equal
probability of being on
any of the great circles
on a sphere. (Check
out the linked video
on Hopf Fibration.)Therefore in relativistic space, we can think of an electron being found on a shell around a nucleus. We keep in mind that we are assuming an ideal case of a circular orbit and a spherical shell. We have not accounted for the rotation and vibration properties of either the electron or the nucleus. We can also ask, if it is possible for the electron to change orbit between great circles, on the shell?
 In
measurement space, it is
not possible to change
direction without being
provided additional
resources. Let us
assume that we provide
the electron with a
change of momentum
p,
with a photon, to shift
the electron into the
neighboring orbit by an
infinitesimal distance
.
In
measurement space, it is
not possible to change
direction without being
provided additional
resources. Let us
assume that we provide
the electron with a
change of momentum
p,
with a photon, to shift
the electron into the
neighboring orbit by an
infinitesimal distance
.
This photon will have the wavelength The momentum change therefore is given as . We can equivalently write , which is the uncertainty principle. Thus the shell structure formed by the electron around the proton in S'-frame, when its momentum is changed, is discrete.
The observer in S-frame may deduce it as infinitely continuous depending upon the measurement limitations. However the shell structure for an electron in S-frame, will be discrete per Heisenberg's uncertainty principle (unless there is an additional mechanism in play).
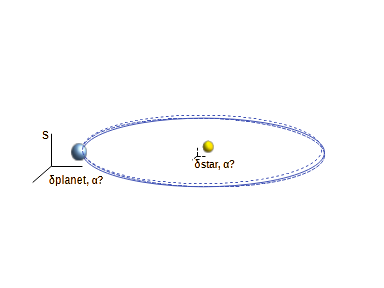 How
about if the observers
in S and S' frames, both
represented composite
-functions?
What if we replaced the
electron in S-frame with
a planet and the proton
in S'-frame with a star?
We do not know the
values
for either
structures.
However it is likely to
be a non-relativistic
case with the star
having much higher
capability.
How
about if the observers
in S and S' frames, both
represented composite
-functions?
What if we replaced the
electron in S-frame with
a planet and the proton
in S'-frame with a star?
We do not know the
values
for either
structures.
However it is likely to
be a non-relativistic
case with the star
having much higher
capability.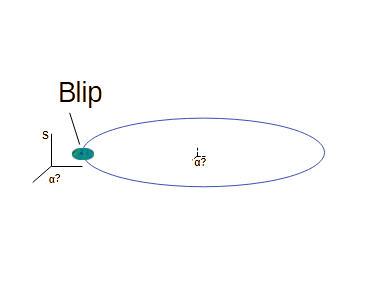 Next, what if the planet
in S-frame is replaced
by Blip, our
universe? This is
a real puzzle, as not
only we do not know
about the
-value
for Blip, we have no
idea what structure
exists in S'-frame?
Next, what if the planet
in S-frame is replaced
by Blip, our
universe? This is
a real puzzle, as not
only we do not know
about the
-value
for Blip, we have no
idea what structure
exists in S'-frame? But we can guesstimate that Blip in S-frame must be circuiting around the S'-frame in a state of measurement, in some sort of an orbit or a shell. Does Blip has its own spin? Is it now a quantum problem or a classical problem?
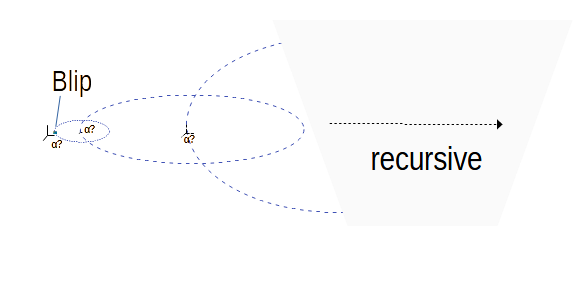 We can
easily think of a
recursive structure as
shown here.
Perhaps the gravity is
more complex than we
thought!
We can
easily think of a
recursive structure as
shown here.
Perhaps the gravity is
more complex than we
thought!The bottom line in the discrete measurement space remains whether the observer in S-frame can complete the measurement circuit Mckt in S'-frame, or not?

In case, the Mckt can not be completed, we have to complete it by the path PQ.5 For now, we will be discussing the case, where Mckt can be completed in S'-frame.
....to
be continued
1. Principle
of least action
2. The curve of least disorder for the path PQ, is not equivalent to the straight line between P and Q.
3. AKU - All Knowing Us, The Bug On Windshield (TB) - infinite momentum frame.
4. We have just introduced two very important concepts, those of Tensor Calculus and Inner Product.
5. Which actually is the problem definition for the discrete measurement space.
2. The curve of least disorder for the path PQ, is not equivalent to the straight line between P and Q.
3. AKU - All Knowing Us, The Bug On Windshield (TB) - infinite momentum frame.
4. We have just introduced two very important concepts, those of Tensor Calculus and Inner Product.
5. Which actually is the problem definition for the discrete measurement space.
Previous Blogs:
The Theory of
Measurements - IV
The Theory of
Measurements - III
An Ecosystem of δ-Potentials -
IVA
An Ecosystem of δ-Potentials - III
An Ecosystem of δ-Potentials - II
An Ecosystem of δ-Potentials - I
Nutshell-2019
Stitching Measurement Space - III
Stitching Measurement Space - II
Stitching Measurement Space - I
Mass Length & Topology
A Timeless Constant
Space Time and Entropy
Nutshell-2018
Curve of Least Disorder
Möbius & Lorentz Transformation - II
Möbius & Lorentz Transformation - I
Knots, DNA & Enzymes
Quantum Comp - III
Nutshell-2017
Quantum Comp - II
Quantum Comp - I
Insincere Symmetry - II
Insincere Symmetry - I
Existence in 3-D
Infinite Source
Nutshell-2016
Quanta-II
Quanta-I
EPR Paradox-II
EPR Paradox-I
De Broglie Equation
Duality in j-space
A Paradox
The Observers
Nutshell-2015
Chiral Symmetry
Sigma-z and I
Spin Matrices
Rationale behind Irrational Numbers
The Ubiquitous z-Axis
An Ecosystem of δ-Potentials - III
An Ecosystem of δ-Potentials - II
An Ecosystem of δ-Potentials - I
Nutshell-2019
Stitching Measurement Space - III
Stitching Measurement Space - II
Stitching Measurement Space - I
Mass Length & Topology
A Timeless Constant
Space Time and Entropy
Nutshell-2018
Curve of Least Disorder
Möbius & Lorentz Transformation - II
Möbius & Lorentz Transformation - I
Knots, DNA & Enzymes
Quantum Comp - III
Nutshell-2017
Quantum Comp - II
Quantum Comp - I
Insincere Symmetry - II
Insincere Symmetry - I
Existence in 3-D
Infinite Source
Nutshell-2016
Quanta-II
Quanta-I
EPR Paradox-II
EPR Paradox-I
De Broglie Equation
Duality in j-space
A Paradox
The Observers
Nutshell-2015
Chiral Symmetry
Sigma-z and I
Spin Matrices
Rationale behind Irrational Numbers
The Ubiquitous z-Axis

Attribution — You must give appropriate credit, provide a link to the license, and indicate if changes were made. You may do so in any reasonable manner, but not in any way that suggests the licensor endorses you or your use. No additional restrictions — You may not apply legal terms or technological measures that legally restrict others from doing anything the license permits. This is a human-readable summary of (and not a substitute for) the license.